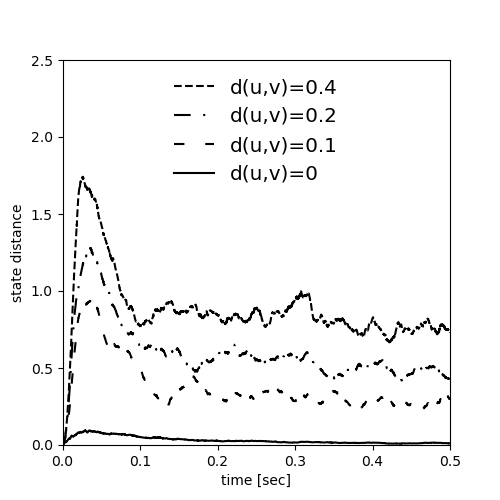
Example: Maass_Natschlaeger_Markram_2002
Fig. 2 from:
Real-Time Computing Without Stable States: A New Framework for Neural Computation Based on Perturbations
Neural Computation 14, 2531–2560 (2002)
by Maass W., Natschläger T. and Markram H.
Sebastian Schmitt, 2022
from collections import defaultdict
import multiprocessing
import numpy as np
import matplotlib.pyplot as plt
from brian2 import (
NeuronGroup,
Synapses,
SpikeGeneratorGroup,
SpikeMonitor,
Network,
prefs,
)
from brian2 import ms, mV, Mohm, nA, second, Hz
from brian2 import defaultclock, prefs
N_NEURONS = 135
V_THRESH = 15 * mV
V_RESET = 13.5 * mV
STIMULUS_POISSON_RATE = 20 * Hz
TARGET_DISTANCES = [0.4, 0.2, 0.1]
N_PAIRS = 200
DT = 0.1 * ms
DURATION = 500 * ms
TS = np.arange(0, DURATION / ms, DT / ms)
def exponential_convolution(t, spikes, tau):
"""Convolute spikes with exponential kernel
t -- numpy array of times to evaluate the convolution
spikes -- iterable of spike times
tau -- exponential decay constant
"""
if len(spikes):
return sum([np.exp(-((t - st) / tau)) * (t >= st) for st in spikes])
else:
return np.zeros(len(TS))
def gaussian_convolution(t, spikes, tau):
"""Convolute spikes with Gaussian kernel
t -- numpy array of times to evaluate the convolution
spikes -- iterable of spike times
tau -- exponential decay constant
"""
if len(spikes):
return sum([np.exp(-(((t - st) / tau) ** 2)) for st in spikes])
else:
return np.zeros(len(TS))
def euclidian_distance(liquid_states_u, liquid_states_v):
"""Euclidian distance between liquid states
liquid_states_u -- liquid states
liquid_states_v -- other liquid states
To match the numbers in the paper, the square root is omitted
"""
return np.mean((liquid_states_u - liquid_states_v) ** 2, axis=0)
def distance(conv_a, conv_b, dt):
"""Difference of convolutions in the L2-norm
conv_a -- convolutions
conv_b -- other convolutions
dt -- time step
To match the numbers in the paper, the square root is omitted
"""
return sum((conv_a - conv_b) ** 2) * dt
def generate_poisson(duration, rate):
"""Generate Poisson spike train
duration -- duration of spike train
rate -- rate of spike train
Return only spike trains that do not have multiple spikes per time bin
"""
while True:
N = np.random.poisson(rate * duration)
spikes = np.random.uniform(0, duration, N)
spikes_orig = np.sort(spikes)
shift = 1e-3 * (DT / ms)
timebins = ((spikes_orig + shift) / (DT / ms)).astype(np.int32)
if not any(np.diff(timebins) == 0):
return spikes_orig
def collect_stimulus_pairs():
"""Collect pairs of input stimuli close in target distance"""
DELTA_DISTANCE = 0.01
collected_pairs = defaultdict(list)
while True:
spikes_u = generate_poisson(DURATION / ms, STIMULUS_POISSON_RATE / Hz / 1e3)
spikes_v = generate_poisson(DURATION / ms, STIMULUS_POISSON_RATE / Hz / 1e3)
conv_u = gaussian_convolution(TS, spikes_u, tau=5)
conv_v = gaussian_convolution(TS, spikes_v, tau=5)
normed_distance = distance(conv_u, conv_v, DT / ms) / (DURATION / ms)
for target_distance in TARGET_DISTANCES:
if (
abs(normed_distance - target_distance) < DELTA_DISTANCE
and len(collected_pairs[target_distance]) < N_PAIRS
):
collected_pairs[target_distance].append((spikes_u, spikes_v))
# stop if we have enough pairs collected
if len(collected_pairs) == len(TARGET_DISTANCES) and all(
np.array(list(map(len, collected_pairs.values()))) == N_PAIRS
):
break
return collected_pairs
def get_neurons():
neurons = NeuronGroup(
N_NEURONS,
"""
tau_mem : second (shared, constant)
tau_refrac : second (constant)
v_reset : volt (shared, constant)
v_thresh : volt (shared, constant)
I_b : ampere (shared, constant)
tau_stimulus : second (constant)
I_syn_ee_synapses : ampere
I_syn_ei_synapses : ampere
I_syn_ie_synapses : ampere
I_syn_ii_synapses : ampere
dI_stimulus/dt = -I_stimulus/tau_stimulus : ampere
R_in : ohm
dv/dt = -v/tau_mem + (I_syn_ee_synapses +
I_syn_ei_synapses +
I_syn_ie_synapses +
I_syn_ii_synapses)*R_in/tau_mem
+ I_b*R_in/tau_mem
+ I_stimulus*R_in/tau_mem: volt (unless refractory)
x_pos : 1 (constant)
y_pos : 1 (constant)
z_pos : 1 (constant)
""",
threshold="v>v_thresh",
reset="v=v_reset",
refractory="tau_refrac",
method="exact",
name="neurons",
)
neurons.tau_mem = 30 * ms
neurons.v_thresh = V_THRESH
neurons.v_reset = V_RESET
neurons.I_b = 13.5 * nA
neurons.v[:] = (
np.random.uniform(V_RESET / mV, V_THRESH / mV, size=len(neurons)) * mV
)
neurons.R_in = 1 * Mohm
# to randomly assign excitatory and inhibitory neurons later
indices = np.arange(len(neurons))
np.random.shuffle(indices)
# a column of 15x3x3 neurons
neurons.x_pos = indices % 3
neurons.y_pos = (indices // 3) % 3
neurons.z_pos = indices // 9
return neurons
def get_synapses(name, source, target, C, l, tau_I, A, U, D, F, delay):
synapses_eqs = """
A : ampere (constant)
U : 1 (constant)
tau_I : second (shared, constant)
D : second (constant)
dx/dt = z/D : 1 (clock-driven) # recovered
dy/dt = -y/tau_I : 1 (clock-driven) # active
z = 1 - x - y : 1 # inactive
I_syn_{}_post = A*y : ampere (summed)
""".format(name)
if F:
synapses_eqs += """
du/dt = -u/F : 1 (clock-driven)
F : second (constant)
"""
synapses_action = """
u += U*(1-u)
y += u*x # important: update y first
x += -u*x
"""
else:
synapses_action = """
y += U*x # important: update y first
x += -U*x
"""
synapses = Synapses(
source,
target,
model=synapses_eqs,
on_pre=synapses_action,
method="exact",
name=name,
delay=delay,
)
synapses.connect(
p=f"{C} * exp(-((x_pos_pre-x_pos_post)**2 + (y_pos_pre-y_pos_post)**2 + (z_pos_pre-z_pos_post)**2)/{l}**2)"
)
N_syn = len(synapses)
synapses.tau_I = tau_I
synapses.A[:] = np.sign(A / nA) * np.random.gamma(1, abs(A / nA), size=N_syn) * nA
synapses.U[:] = np.random.normal(U, 0.5, size=N_syn)
# paper samples from uniform, we take the mean
synapses.U[:][synapses.U < 0] = U
synapses.D[:] = np.random.normal(D / ms, 0.5 * D / ms, size=N_syn) * ms
# paper samples from uniform, we take the mean
synapses.D[:][synapses.D / ms <= 0] = D
# start fully recovered
synapses.x = 1
if F:
synapses.F[:] = np.random.normal(F / ms, 0.5 * F / ms, size=N_syn) * ms
# paper samples from uniform, we take the mean
synapses.F[:][synapses.F / ms <= 0] = F
return synapses
def sim(net, spike_times):
"""Run network with given stimulus
Redraws initial membrane voltages
net -- the network to simulate
spike_times -- the stimulus to inject
"""
net.restore()
net["neurons"].v = (
np.random.uniform(V_RESET / mV, V_THRESH / mV, size=len(neurons)) * mV
)
net["stimulus"].set_spikes([0] * len(spike_times), spike_times * ms)
net.run(DURATION)
spikes = list(net["spike_monitor_exc"].spike_trains().values()) + list(
net["spike_monitor_inh"].spike_trains().values()
)
liquid_states = np.array(
[exponential_convolution(TS, st / ms, tau=30) for st in spikes]
)
return liquid_states
if __name__ == '__main__':
neurons = get_neurons()
N_exc = int(0.8 * len(neurons))
exc_neurons = neurons[:N_exc]
exc_neurons.tau_refrac = 3 * ms
exc_neurons.tau_stimulus = 3 * ms
inh_neurons = neurons[N_exc:]
inh_neurons.tau_refrac = 2 * ms
inh_neurons.tau_stimulus = 6 * ms
l_lambda = 2
ee_synapses = get_synapses(
"ee_synapses",
exc_neurons,
exc_neurons,
C=0.3,
l=l_lambda,
tau_I=3 * ms,
A=30 * nA,
U=0.5,
D=1.1 * second,
F=0.05 * second,
delay=1.5 * ms,
)
ei_synapses = get_synapses(
"ei_synapses",
exc_neurons,
inh_neurons,
C=0.2,
l=l_lambda,
tau_I=3 * ms,
A=60 * nA,
U=0.05,
D=0.125 * second,
F=1.2 * second,
delay=0.8 * ms,
)
ie_synapses = get_synapses(
"ie_synapses",
inh_neurons,
exc_neurons,
C=0.4,
l=l_lambda,
tau_I=6 * ms,
A=-19 * nA,
U=0.25,
D=0.7 * second,
F=0.02 * second,
delay=0.8 * ms,
)
ii_synapses = get_synapses(
"ii_synapses",
inh_neurons,
inh_neurons,
C=0.1,
l=l_lambda,
tau_I=6 * ms,
A=-19 * nA,
U=0.32,
D=0.144 * second,
F=0.06 * second,
delay=0.8 * ms,
)
# place holder for stimulus
stimulus = SpikeGeneratorGroup(1, [], [] * ms, name="stimulus")
spike_monitor_stimulus = SpikeMonitor(stimulus)
static_synapses_exc = Synapses(
stimulus,
exc_neurons,
"A : ampere (shared, constant)",
on_pre="I_stimulus += A"
)
static_synapses_exc.connect(p=1)
static_synapses_exc.A = 18 * nA
static_synapses_inh = Synapses(
stimulus,
inh_neurons,
"A : ampere (shared, constant)",
on_pre="I_stimulus += A"
)
static_synapses_inh.connect(p=1)
static_synapses_inh.A = 9 * nA
spike_monitor_exc = SpikeMonitor(exc_neurons, name="spike_monitor_exc")
spike_monitor_inh = SpikeMonitor(inh_neurons, name="spike_monitor_inh")
defaultclock.dt = DT
net = Network(
[
neurons,
ee_synapses,
ei_synapses,
ie_synapses,
ii_synapses,
static_synapses_exc,
static_synapses_inh,
stimulus,
spike_monitor_exc,
spike_monitor_inh,
]
)
net.store()
collected_pairs = collect_stimulus_pairs()
# add only jittered pairs
collected_pairs[0] = [
[generate_poisson(DURATION / ms, STIMULUS_POISSON_RATE / Hz / 1e3)] * 2
for _ in range(N_PAIRS)
]
def map_sim(spike_times):
"""Wrapper to sim for multiprocessing
"""
return sim(net, spike_times)
result = defaultdict(list)
# loop over all distances and Poisson stimulus pairs
for d, pairs in collected_pairs.items():
with multiprocessing.Pool() as p:
states_u = p.map(map_sim, [p[0] for p in pairs])
states_v = p.map(map_sim, [p[1] for p in pairs])
for liquid_states_u, liquid_states_v in zip(states_u, states_v):
ed = euclidian_distance(liquid_states_u, liquid_states_v)
result[d].append(ed)
# plot
fig, ax = plt.subplots(figsize=(5, 5))
linestyles = ["dashed", (0, (8, 6, 1, 6)), (0, (5, 10)), "solid"]
for d, ls in zip(TARGET_DISTANCES + [0], linestyles):
eds = result[d]
eds = np.array(eds)
ax.plot(
TS / 1000, np.mean(eds, axis=0), label=f"d(u,v)={d}", linestyle=ls, color="k"
)
ax.set_xlabel("time [sec]")
ax.set_ylabel("state distance")
ax.set_xlim(0, 0.5)
ax.set_ylim(0, 2.5)
ax.legend(loc="upper center", fontsize="x-large", frameon=False)
plt.show()