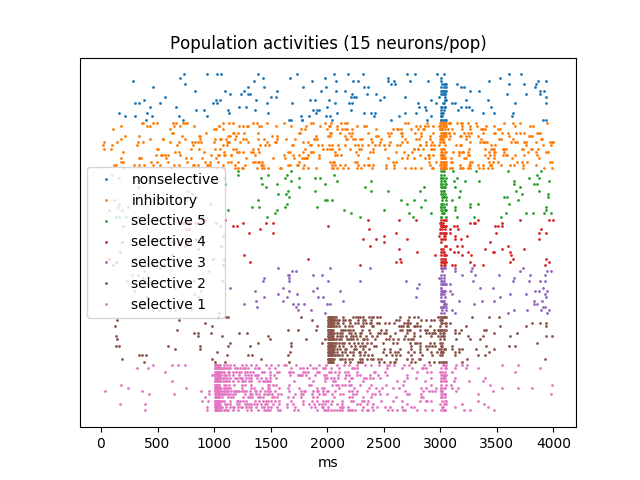
Example: Brunel_Wang_2001

Note

You can launch an interactive, editable version of this example without installing any local files using the Binder service (although note that at some times this may be slow or fail to open):

Sample-specific persistent activity

Five subpopulations with three selective and one reset stimuli example. Analog to figure 6b in the paper.

BRUNEL, Nicolas et WANG, Xiao-Jing. Effects of neuromodulation in a cortical network model of object working memory dominated by recurrent inhibition. Journal of computational neuroscience, 2001, vol. 11, no 1, p. 63-85.

from brian2 import *

# populations
N = 1000
N_E = int(N * 0.8)  # pyramidal neurons
N_I = int(N * 0.2)  # interneurons

# voltage
V_L = -70. * mV
V_thr = -50. * mV
V_reset = -55. * mV
V_E = 0. * mV
V_I = -70. * mV

# membrane capacitance
C_m_E = 0.5 * nF
C_m_I = 0.2 * nF

# membrane leak
g_m_E = 25. * nS
g_m_I = 20. * nS

# refractory period
tau_rp_E = 2. * ms
tau_rp_I = 1. * ms

# external stimuli
rate = 3 * Hz
C_ext = 800

# synapses
C_E = N_E
C_I = N_I

# AMPA (excitatory)
g_AMPA_ext_E = 2.08 * nS
g_AMPA_rec_E = 0.104 * nS * 800. / N_E
g_AMPA_ext_I = 1.62 * nS
g_AMPA_rec_I = 0.081 * nS * 800. / N_E
tau_AMPA = 2. * ms

# NMDA (excitatory)
g_NMDA_E = 0.327 * nS * 800. / N_E
g_NMDA_I = 0.258 * nS * 800. / N_E
tau_NMDA_rise = 2. * ms
tau_NMDA_decay = 100. * ms
alpha = 0.5 / ms
Mg2 = 1.

# GABAergic (inhibitory)
g_GABA_E = 1.25 * nS * 200. / N_I
g_GABA_I = 0.973 * nS * 200. / N_I
tau_GABA = 10. * ms

# subpopulations
f = 0.1
p = 5
N_sub = int(N_E * f)
N_non = int(N_E * (1. - f * p))
w_plus = 2.1
w_minus = 1. - f * (w_plus - 1.) / (1. - f)

# modeling
eqs_E = '''
dv / dt = (- g_m_E * (v - V_L) - I_syn) / C_m_E : volt (unless refractory)

I_syn = I_AMPA_ext + I_AMPA_rec + I_NMDA_rec + I_GABA_rec : amp

I_AMPA_ext = g_AMPA_ext_E * (v - V_E) * s_AMPA_ext : amp
I_AMPA_rec = g_AMPA_rec_E * (v - V_E) * 1 * s_AMPA : amp
ds_AMPA_ext / dt = - s_AMPA_ext / tau_AMPA : 1
ds_AMPA / dt = - s_AMPA / tau_AMPA : 1

I_NMDA_rec = g_NMDA_E * (v - V_E) / (1 + Mg2 * exp(-0.062 * v / mV) / 3.57) * s_NMDA_tot : amp
s_NMDA_tot : 1

I_GABA_rec = g_GABA_E * (v - V_I) * s_GABA : amp
ds_GABA / dt = - s_GABA / tau_GABA : 1
'''

eqs_I = '''
dv / dt = (- g_m_I * (v - V_L) - I_syn) / C_m_I : volt (unless refractory)

I_syn = I_AMPA_ext + I_AMPA_rec + I_NMDA_rec + I_GABA_rec : amp

I_AMPA_ext = g_AMPA_ext_I * (v - V_E) * s_AMPA_ext : amp
I_AMPA_rec = g_AMPA_rec_I * (v - V_E) * 1 * s_AMPA : amp
ds_AMPA_ext / dt = - s_AMPA_ext / tau_AMPA : 1
ds_AMPA / dt = - s_AMPA / tau_AMPA : 1

I_NMDA_rec = g_NMDA_I * (v - V_E) / (1 + Mg2 * exp(-0.062 * v / mV) / 3.57) * s_NMDA_tot : amp
s_NMDA_tot : 1

I_GABA_rec = g_GABA_I * (v - V_I) * s_GABA : amp
ds_GABA / dt = - s_GABA / tau_GABA : 1
'''

P_E = NeuronGroup(N_E, eqs_E, threshold='v > V_thr', reset='v = V_reset', refractory=tau_rp_E, method='euler')
P_E.v = V_L
P_I = NeuronGroup(N_I, eqs_I, threshold='v > V_thr', reset='v = V_reset', refractory=tau_rp_I, method='euler')
P_I.v = V_L

eqs_glut = '''
s_NMDA_tot_post = w * s_NMDA : 1 (summed)
ds_NMDA / dt = - s_NMDA / tau_NMDA_decay + alpha * x * (1 - s_NMDA) : 1 (clock-driven)
dx / dt = - x / tau_NMDA_rise : 1 (clock-driven)
w : 1
'''

eqs_pre_glut = '''
s_AMPA += w
x += 1
'''

eqs_pre_gaba = '''
s_GABA += 1
'''

# E to E
C_E_E = Synapses(P_E, P_E, model=eqs_glut, on_pre=eqs_pre_glut, method='euler')
C_E_E.connect('i != j')
C_E_E.w[:] = 1

for pi in range(N_non, N_non + p * N_sub, N_sub):

    # internal other subpopulation to current nonselective
    C_E_E.w[C_E_E.indices[:, pi:pi + N_sub]] = w_minus

    # internal current subpopulation to current subpopulation
    C_E_E.w[C_E_E.indices[pi:pi + N_sub, pi:pi + N_sub]] = w_plus

# E to I
C_E_I = Synapses(P_E, P_I, model=eqs_glut, on_pre=eqs_pre_glut, method='euler')
C_E_I.connect()
C_E_I.w[:] = 1

# I to I
C_I_I = Synapses(P_I, P_I, on_pre=eqs_pre_gaba, method='euler')
C_I_I.connect('i != j')

# I to E
C_I_E = Synapses(P_I, P_E, on_pre=eqs_pre_gaba, method='euler')
C_I_E.connect()

# external noise
C_P_E = PoissonInput(P_E, 's_AMPA_ext', C_ext, rate, '1')
C_P_I = PoissonInput(P_I, 's_AMPA_ext', C_ext, rate, '1')

# at 1s, select population 1
C_selection = int(f * C_ext)
rate_selection = 25 * Hz
stimuli1 = TimedArray(np.r_[np.zeros(40), np.ones(2), np.zeros(100)], dt=25 * ms)
input1 = PoissonInput(P_E[N_non:N_non + N_sub], 's_AMPA_ext', C_selection, rate_selection, 'stimuli1(t)')

# at 2s, select population 2
stimuli2 = TimedArray(np.r_[np.zeros(80), np.ones(2), np.zeros(100)], dt=25 * ms)
input2 = PoissonInput(P_E[N_non + N_sub:N_non + 2 * N_sub], 's_AMPA_ext', C_selection, rate_selection, 'stimuli2(t)')

# at 4s, reset selection
stimuli_reset = TimedArray(np.r_[np.zeros(120), np.ones(2), np.zeros(100)], dt=25 * ms)
input_reset_I = PoissonInput(P_E, 's_AMPA_ext', C_ext, rate_selection, 'stimuli_reset(t)')
input_reset_E = PoissonInput(P_I, 's_AMPA_ext', C_ext, rate_selection, 'stimuli_reset(t)')

# monitors
N_activity_plot = 15
sp_E_sels = [SpikeMonitor(P_E[pi:pi + N_activity_plot]) for pi in range(N_non, N_non + p * N_sub, N_sub)]
sp_E = SpikeMonitor(P_E[:N_activity_plot])
sp_I = SpikeMonitor(P_I[:N_activity_plot])

r_E_sels = [PopulationRateMonitor(P_E[pi:pi + N_sub]) for pi in range(N_non, N_non + p * N_sub, N_sub)]
r_E = PopulationRateMonitor(P_E[:N_non])
r_I = PopulationRateMonitor(P_I)

# simulate, can be long >120s
net = Network(collect())
net.add(sp_E_sels)
net.add(r_E_sels)
net.run(4 * second, report='stdout')

# plotting
title('Population rates')
xlabel('ms')
ylabel('Hz')

plot(r_E.t / ms, r_E.smooth_rate(width=25 * ms) / Hz, label='nonselective')
plot(r_I.t / ms, r_I.smooth_rate(width=25 * ms) / Hz, label='inhibitory')

for i, r_E_sel in enumerate(r_E_sels[::-1]):
    plot(r_E_sel.t / ms, r_E_sel.smooth_rate(width=25 * ms) / Hz,
         label=f"selective {p - i}")

legend()
figure()

title(f"Population activities ({N_activity_plot} neurons/pop)")
xlabel('ms')
yticks([])

plot(sp_E.t / ms, sp_E.i + (p + 1) * N_activity_plot, '.', markersize=2,
     label="nonselective")
plot(sp_I.t / ms, sp_I.i + p * N_activity_plot, '.', markersize=2, label="inhibitory")

for i, sp_E_sel in enumerate(sp_E_sels[::-1]):
    plot(sp_E_sel.t / ms, sp_E_sel.i + (p - i - 1) * N_activity_plot, '.', markersize=2,
         label=f"selective {p - i}")

legend()
show()