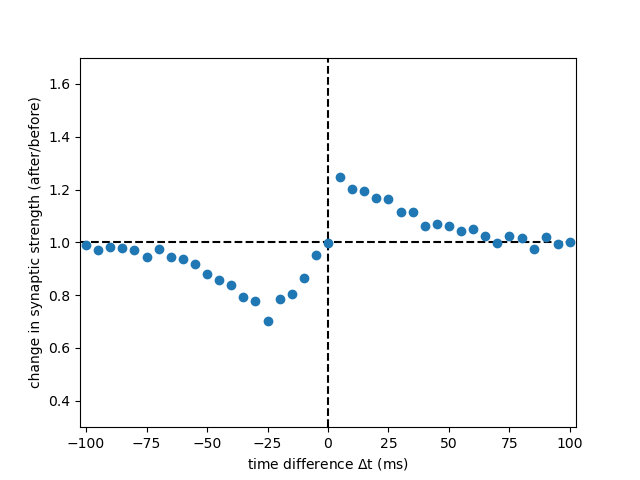
Example: Graupner_Brunel_2012
Fig. 2 C, panel DP from:
Calcium-based plasticity model explains sensitivity of synaptic changes to spike pattern, rate, and dendritic location
PNAS 109 (10): 3991-3996 (2012) https://doi.org/10.1073/pnas.1109359109
by Graupner M. and Brunel N. (2012)
For the noise term see corrections https://www.pnas.org/doi/10.1073/pnas.1220044110.
For the original implementations see https://github.com/mgraupe/CalciumBasedPlasticityModel/tree/main/Graupner2012PNAS.
Sebastian Schmitt, 2022
import multiprocessing
import numpy as np
import matplotlib.pyplot as plt
from brian2 import NeuronGroup, Synapses
from brian2 import ms, second
from brian2 import run
# number of time differences in STDP plot
POINTS = 41
# maximal time difference
STDP_DT_MAX = 100 * ms
# (symmetric) minimal time difference
STDP_DT_MIN = -STDP_DT_MAX
# number of repetitions
REPETITIONS = 1000
# time difference step size
STDP_DT_STEP = (STDP_DT_MAX - STDP_DT_MIN) / (POINTS - 1)
def run_sim(point_index):
"""Run simulation for one STDP time difference"""
# Cf. https://brian2.readthedocs.io/en/stable/resources/tutorials/2-intro-to-brian-synapses.html#more-complex-synapse-models-stdp
# set up two groups of neurons, G spikes at fixed times starting from STDP_DT_MAX
# H spikes shifted according to point_index and has as many neurons as REPETITIONS*2
# (we need to multiply by 2 for both initial states (UP and DOWN))
# G: |
# H: |
# H: |
# H: |
# ...
G = NeuronGroup(1, "", threshold=f"t>{STDP_DT_MAX/ms}*ms", refractory=1 * second)
H = NeuronGroup(
REPETITIONS * 2, "tspike:second", threshold="t>tspike", refractory=1 * second
)
H.tspike = [point_index * STDP_DT_STEP] * REPETITIONS * 2
synapses_eqs = """
tau : second (constant, shared)
rho_star : 1 (constant, shared)
gamma_p : 1 (constant, shared)
theta_p : 1 (constant, shared)
gamma_d : 1 (constant, shared)
theta_d : 1 (constant, shared)
drho/dt = (-rho*(1-rho)*(rho_star-rho)
+ gamma_p*(1-rho)*int((c - theta_p) > 0)
- gamma_d*rho*int((c-theta_d) > 0)
+ sigma*sqrt(tau)*sqrt(int((c-theta_d) > 0) + int((c-theta_p) > 0))*xi
) / tau : 1 (clock-driven)
dc/dt = -c/tau_Ca : 1 (clock-driven)
tau_Ca : second (constant, shared)
sigma : 1 (constant, shared)
"""
C_pre = 1
C_post = 2
D = 13.7 * ms
synapses = Synapses(
G,
H,
model=synapses_eqs,
on_pre="c += C_pre",
on_post="c += C_post",
delay=D,
method="heun",
)
synapses.connect()
synapses.tau_Ca = 20 * ms
synapses.theta_d = 1
synapses.theta_p = 1.3
synapses.gamma_d = 200
synapses.gamma_p = 321.808
synapses.sigma = 2.8284
synapses.tau = 150 * second
synapses.rho_star = 0.5
# start with equal number of synapses in DOWN and UP state
# must match b in analysis below
rho_initial = np.array([0] * REPETITIONS + [1] * REPETITIONS)
synapses.rho = rho_initial
def report_callback(elapsed, completed, start, duration):
print(
f"time difference {(point_index*STDP_DT_STEP - STDP_DT_MAX)/ms:.0f} ms is {completed:2.0%} done"
)
run(60 * second, report=report_callback)
return synapses.rho[:], rho_initial
if __name__ == "__main__":
with multiprocessing.Pool() as p:
results = p.map(run_sim, range(POINTS))
# initial fraction of synapses in DOWN state
beta = 0.5
# ratio of UP and DOWN state weights (w1/w0)
b = 5
change_in_syn_strengths = []
for rhos, rhos_initial in results:
# average switching probabilities
U = np.mean(rhos[rhos_initial < 0.5] > 0.5)
D = np.mean(rhos[rhos_initial > 0.5] < 0.5)
change_in_syn_strength = (
(1 - U) * beta + D * (1 - beta) + b * (U * beta + (1 - D) * (1 - beta))
) / (beta + (1 - beta) * b)
change_in_syn_strengths.append(change_in_syn_strength)
stdp_dts = [
point_index * STDP_DT_STEP - STDP_DT_MAX for point_index in range(POINTS)
]
plt.axvline(0, linestyle="dashed", color="k")
plt.axhline(1, linestyle="dashed", color="k")
plt.plot(stdp_dts / ms, change_in_syn_strengths, marker="o", linestyle="None")
plt.xlim(
(STDP_DT_MIN - STDP_DT_STEP / 2) / ms, (STDP_DT_MAX + STDP_DT_STEP / 2) / ms
)
plt.ylim(0.3, 1.7)
plt.xlabel(r"time difference $\Delta$t (ms)")
plt.ylabel("change in synaptic strength (after/before)")
plt.show()