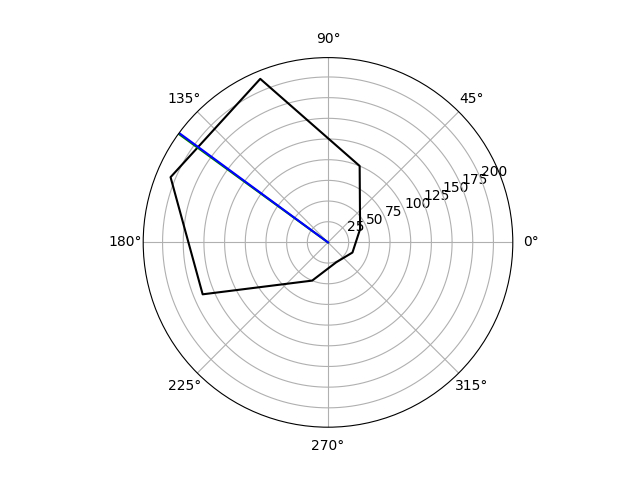
Example: Sturzl_et_al_2000

Note

You can launch an interactive, editable version of this example without installing any local files using the Binder service (although note that at some times this may be slow or fail to open):

Adapted from Theory of Arachnid Prey Localization W. Sturzl, R. Kempter, and J. L. van Hemmen PRL 2000

Poisson inputs are replaced by integrate-and-fire neurons

Romain Brette

from brian2 import *

# Parameters
degree = 2 * pi / 360.
duration = 500*ms
R = 2.5*cm  # radius of scorpion
vr = 50*meter/second  # Rayleigh wave speed
phi = 144*degree  # angle of prey
A = 250*Hz
deltaI = .7*ms  # inhibitory delay
gamma = (22.5 + 45 * arange(8)) * degree  # leg angle
delay = R / vr * (1 - cos(phi - gamma))   # wave delay

# Wave (vector w)
time = arange(int(duration / defaultclock.dt) + 1) * defaultclock.dt
Dtot = 0.
w = 0.
for f in arange(150, 451)*Hz:
    D = exp(-(f/Hz - 300) ** 2 / (2 * (50 ** 2)))
    rand_angle = 2 * pi * rand()
    w += 100 * D * cos(2 * pi * f * time + rand_angle)
    Dtot += D
w = .01 * w / Dtot

# Rates from the wave
rates = TimedArray(w, dt=defaultclock.dt)

# Leg mechanical receptors
tau_legs = 1 * ms
sigma = .01
eqs_legs = """
dv/dt = (1 + rates(t - d) - v)/tau_legs + sigma*(2./tau_legs)**.5*xi:1
d : second
"""
legs = NeuronGroup(8, model=eqs_legs, threshold='v > 1', reset='v = 0',
                   refractory=1*ms, method='euler')
legs.d = delay
spikes_legs = SpikeMonitor(legs)

# Command neurons
tau = 1 * ms
taus = 1.001 * ms
wex = 7
winh = -2
eqs_neuron = '''
dv/dt = (x - v)/tau : 1
dx/dt = (y - x)/taus : 1 # alpha currents
dy/dt = -y/taus : 1
'''
neurons = NeuronGroup(8, model=eqs_neuron, threshold='v>1', reset='v=0',
                      method='exact')
synapses_ex = Synapses(legs, neurons, on_pre='y+=wex')
synapses_ex.connect(j='i')
synapses_inh = Synapses(legs, neurons, on_pre='y+=winh', delay=deltaI)
synapses_inh.connect('abs(((j - i) % N_post) - N_post/2) <= 1')
spikes = SpikeMonitor(neurons)

run(duration, report='text')

nspikes = spikes.count
phi_est = imag(log(sum(nspikes * exp(gamma * 1j))))
print("True angle (deg): %.2f" % (phi/degree))
print("Estimated angle (deg): %.2f" % (phi_est/degree))
rmax = amax(nspikes)/duration/Hz
polar(concatenate((gamma, [gamma[0] + 2 * pi])),
      concatenate((nspikes, [nspikes[0]])) / duration / Hz,
      c='k')
axvline(phi, ls='-', c='g')
axvline(phi_est, ls='-', c='b')
show()