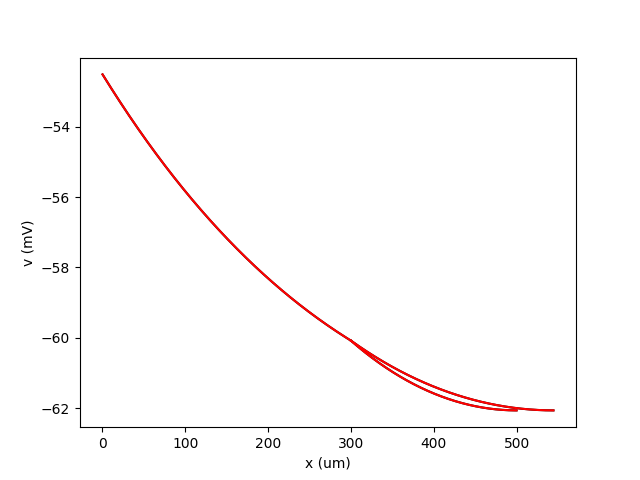
Example: rall

Note

You can launch an interactive, editable version of this example without installing any local files using the Binder service (although note that at some times this may be slow or fail to open):

A cylinder plus two branches, with diameters according to Rall’s formula

from brian2 import *

defaultclock.dt = 0.01*ms

# Passive channels
gL = 1e-4*siemens/cm**2
EL = -70*mV

# Morphology
diameter = 1*um
length = 300*um
Cm = 1*uF/cm**2
Ri = 150*ohm*cm
N = 500
rm = 1 / (gL * pi * diameter)  # membrane resistance per unit length
ra = (4 * Ri)/(pi * diameter**2)  # axial resistance per unit length
la = sqrt(rm / ra) # space length
morpho = Cylinder(diameter=diameter, length=length, n=N)
d1 = 0.5*um
L1 = 200*um
rm = 1 / (gL * pi * d1) # membrane resistance per unit length
ra = (4 * Ri) / (pi * d1**2) # axial resistance per unit length
l1 = sqrt(rm / ra) # space length
morpho.L = Cylinder(diameter=d1, length=L1, n=N)
d2 = (diameter**1.5 - d1**1.5)**(1. / 1.5)
rm = 1/(gL * pi * d2) # membrane resistance per unit length
ra = (4 * Ri) / (pi * d2**2) # axial resistance per unit length
l2 = sqrt(rm / ra) # space length
L2 = (L1 / l1) * l2
morpho.R = Cylinder(diameter=d2, length=L2, n=N)

eqs='''
Im = gL * (EL-v) : amp/meter**2
I : amp (point current)
'''

neuron = SpatialNeuron(morphology=morpho, model=eqs, Cm=Cm, Ri=Ri,
                       method='exponential_euler')
neuron.v = EL

neuron.I[0] = 0.02*nA # injecting at the left end
run(100*ms, report='text')

plot(neuron.main.distance/um, neuron.main.v/mV, 'k')
plot(neuron.L.distance/um, neuron.L.v/mV, 'k')
plot(neuron.R.distance/um, neuron.R.v/mV, 'k')
# Theory
x = neuron.main.distance
ra = la * 4 * Ri/(pi * diameter**2)
l = length/la + L1/l1
theory = EL + ra*neuron.I[0]*cosh(l - x/la)/sinh(l)
plot(x/um, theory/mV, 'r')
x = neuron.L.distance
theory = (EL+ra*neuron.I[0]*cosh(l - neuron.main.distance[-1]/la -
                                 (x - neuron.main.distance[-1])/l1)/sinh(l))
plot(x/um, theory/mV, 'r')
x = neuron.R.distance
theory = (EL+ra*neuron.I[0]*cosh(l - neuron.main.distance[-1]/la -
                                 (x - neuron.main.distance[-1])/l2)/sinh(l))
plot(x/um, theory/mV, 'r')
xlabel('x (um)')
ylabel('v (mV)')
show()