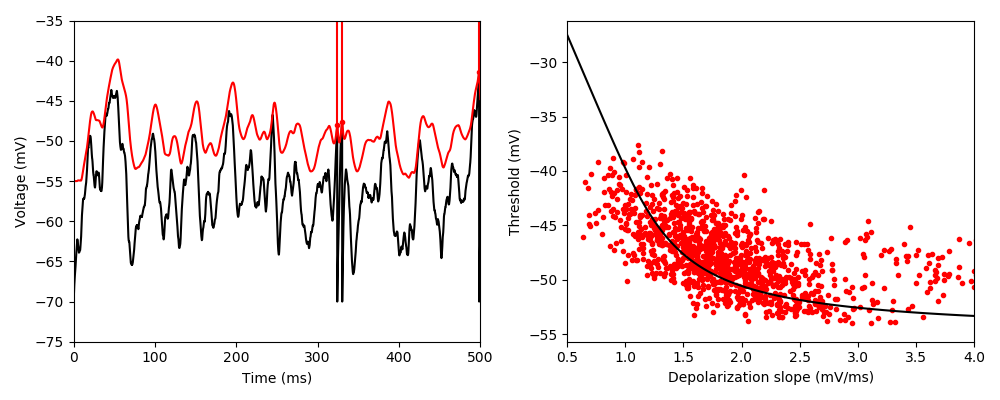
Example: Platkiewicz_Brette_2011

Note

You can launch an interactive, editable version of this example without installing any local files using the Binder service (although note that at some times this may be slow or fail to open):

Slope-threshold relationship with noisy inputs, in the adaptive threshold model

Fig. 5E,F from:

Platkiewicz J and R Brette (2011). Impact of Fast Sodium Channel Inactivation on Spike Threshold Dynamics and Synaptic Integration. PLoS Comp Biol 7(5): e1001129. doi:10.1371/journal.pcbi.1001129

from scipy import optimize
from scipy.stats import linregress

from brian2 import *

N = 200  # 200 neurons to get more statistics, only one is shown
duration = 1*second
# --Biophysical parameters
ENa = 60*mV
EL = -70*mV
vT = -55*mV
Vi = -63*mV
tauh = 5*ms
tau = 5*ms
ka = 5*mV
ki = 6*mV
a = ka / ki
tauI = 5*ms
mu = 15*mV
sigma = 6*mV / sqrt(tauI / (tauI + tau))

# --Theoretical prediction for the slope-threshold relationship (approximation: a=1+epsilon)
thresh = lambda slope, a: Vi - slope * tauh * log(1 + (Vi - vT / a) / (slope * tauh))
# -----Exact calculation of the slope-threshold relationship
# (note that optimize.fsolve does not work with units, we therefore let th be a
# unitless quantity, i.e. the value in volt).
thresh_ex = lambda s: optimize.fsolve(lambda th: (a*s*tauh*exp((Vi-th*volt)/(s*tauh))-th*volt*(1-a)-a*(s*tauh+Vi)+vT)/volt,
                                    thresh(s, a))*volt

eqs = """
dv/dt=(EL-v+mu+sigma*I)/tau : volt
dtheta/dt=(vT+a*clip(v-Vi, 0*mV, inf*mV)-theta)/tauh : volt
dI/dt=-I/tauI+(2/tauI)**.5*xi : 1 # Ornstein-Uhlenbeck
"""
neurons = NeuronGroup(N, eqs, threshold="v>theta", reset='v=EL',
                      refractory=5*ms)
neurons.v = EL
neurons.theta = vT
neurons.I = 0
S = SpikeMonitor(neurons)
M = StateMonitor(neurons, 'v', record=True)
Mt = StateMonitor(neurons, 'theta', record=0)

run(duration, report='text')

# Linear regression gives depolarization slope before spikes
tx = M.t[(M.t > 0*second) & (M.t < 1.5 * tauh)]
slope, threshold = [], []

for (i, t) in zip(S.i, S.t):
    ind = (M.t < t) & (M.t > t - tauh)
    mx = M.v[i, ind]
    s, _, _, _, _ = linregress(tx[:len(mx)]/ms, mx/mV)
    slope.append(s)
    threshold.append(mx[-1])

# Figure
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4))

ax1.plot(M.t/ms, M.v[0]/mV, 'k')
ax1.plot(Mt.t/ms, Mt.theta[0]/mV, 'r')
# Display spikes on the trace
spike_timesteps = np.round(S.t[S.i == 0]/defaultclock.dt).astype(int)
ax1.vlines(S.t[S.i == 0]/ms,
           M.v[0, spike_timesteps]/mV,
           0, color='r')
ax1.plot(S.t[S.i == 0]/ms, M.v[0, spike_timesteps]/mV, 'ro', ms=3)
ax1.set(xlabel='Time (ms)', ylabel='Voltage (mV)', xlim=(0, 500),
        ylim=(-75, -35))

ax2.plot(slope, Quantity(threshold)/mV, 'r.')
sx = linspace(0.5*mV/ms, 4*mV/ms, 100)
t = Quantity([thresh_ex(s) for s in sx])
ax2.plot(sx/(mV/ms), t/mV, 'k')
ax2.set(xlim=(0.5, 4), xlabel='Depolarization slope (mV/ms)',
        ylabel='Threshold (mV)')

fig.tight_layout()
plt.show()