Example: Clopath_et_al_2010_no_homeostasis
Note
You can launch an interactive, editable version of this example without installing any local files using the Binder service (although note that at some times this may be slow or fail to open):
This code contains an adapted version of the voltage-dependent triplet STDP rule from: Clopath et al., Connectivity reflects coding: a model of voltage-based STDP with homeostasis, Nature Neuroscience, 2010 (http://dx.doi.org/10.1038/nn.2479)
The plasticity rule is adapted for a leaky integrate & fire model in
Brian2. In particular, the filters v_lowpass1 and v_lowpass2 are
incremented by a constant at every post-synaptic spike time, to
compensate for the lack of an actual spike in the integrate & fire
model. Moreover, this script does not include the homeostatic
metaplasticity.
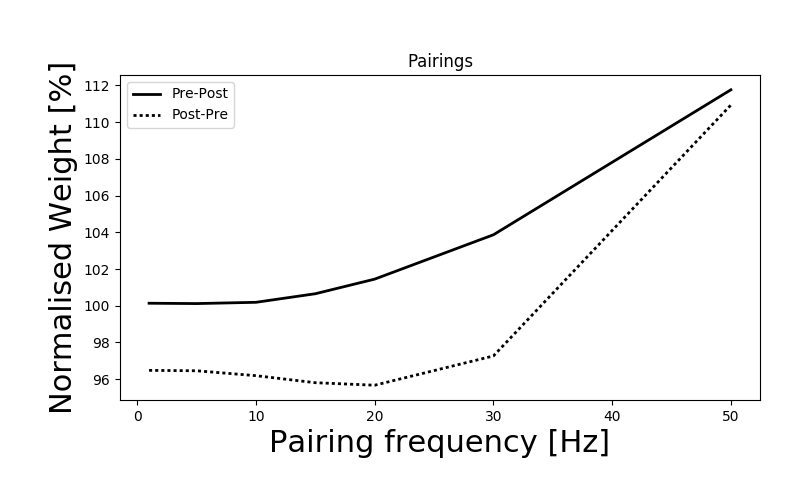
As an illustration of the Rule, we simulate a plot analogous to figure 2b in the above article, showing the frequency dependence of plasticity as measured in: Sjöström et al., Rate, timing and cooperativity jointly determine cortical synaptic plasticity. Neuron, 2001. We would like to note that the parameters have been chosen arbitrarily to qualitatively reproduce the behavior of the original works, but need additional fitting.
We kindly ask to cite both articles when using the model presented below.
This code was written by Jacopo Bono, 12/2015
from brian2 import *
################################################################################
# PLASTICITY MODEL
################################################################################
#### Plasticity Parameters
V_rest = -70.*mV # resting potential
V_thresh = -50.*mV # spiking threshold
Theta_low = V_rest # depolarization threshold for plasticity
x_reset = 1. # spike trace reset value
taux = 15.*ms # spike trace time constant
A_LTD = 1.5e-4 # depression amplitude
A_LTP = 1.5e-2 # potentiation amplitude
tau_lowpass1 = 40*ms # timeconstant for low-pass filtered voltage
tau_lowpass2 = 30*ms # timeconstant for low-pass filtered voltage
#### Plasticity Equations
# equations executed at every timestep
Syn_model = '''
w_ampa:1 # synaptic weight (ampa synapse)
'''
# equations executed only when a presynaptic spike occurs
Pre_eq = '''
g_ampa_post += w_ampa*ampa_max_cond # increment synaptic conductance
w_minus = A_LTD*(v_lowpass1_post/mV - Theta_low/mV)*int(v_lowpass1_post/mV - Theta_low/mV > 0) # synaptic depression
w_ampa = clip(w_ampa-w_minus,0,w_max) # hard bounds
'''
# equations executed only when a postsynaptic spike occurs
Post_eq = '''
v_lowpass1 += 10*mV # mimics the depolarisation by a spike
v_lowpass2 += 10*mV # mimics the depolarisation by a spike
w_plus = A_LTP*x_trace_pre*(v_lowpass2_post/mV - Theta_low/mV)*int(v_lowpass2_post/mV - Theta_low/mV > 0) # synaptic potentiation
w_ampa = clip(w_ampa+w_plus,0,w_max) # hard bounds
'''
################################################################################
# I&F Parameters and equations
################################################################################
#### Neuron parameters
gleak = 30.*nS # leak conductance
C = 300.*pF # membrane capacitance
tau_AMPA = 2.*ms # AMPA synaptic timeconstant
E_AMPA = 0.*mV # reversal potential AMPA
ampa_max_cond = 5.e-10*siemens # Ampa maximal conductance
w_max = 1. # maximal ampa weight
#### Neuron Equations
eqs_neurons = '''
dv/dt = (gleak*(V_rest-v) + I_ext + I_syn)/C: volt # voltage
dv_lowpass1/dt = (v-v_lowpass1)/tau_lowpass1 : volt # low-pass filter of the voltage
dv_lowpass2/dt = (v-v_lowpass2)/tau_lowpass2 : volt # low-pass filter of the voltage
I_ext : amp # external current
I_syn = g_ampa*(E_AMPA-v): amp # synaptic current
dg_ampa/dt = -g_ampa/tau_AMPA : siemens # synaptic conductance
dx_trace/dt = -x_trace/taux :1 # spike trace
'''
################################################################################
# Simulation
################################################################################
#### Parameters
defaultclock.dt = 100.*us # timestep
Nr_neurons = 2 # Number of neurons
rate_array = [1., 5., 10., 15., 20., 30., 50.]*Hz # Rates
init_weight = 0.5 # initial synaptic weight
reps = 15 # Number of pairings
#### Create neuron objects
Nrns = NeuronGroup(Nr_neurons, eqs_neurons, threshold='v>V_thresh',
reset='v=V_rest;x_trace+=x_reset/(taux/ms)', method='euler')#
#### create Synapses
Syn = Synapses(Nrns, Nrns,
model=Syn_model,
on_pre=Pre_eq,
on_post=Post_eq
)
Syn.connect('i!=j')
#### Monitors and storage
weight_result = np.zeros((2, len(rate_array))) # to save the final weights
#### Run
# loop over rates
for jj, rate in enumerate(rate_array):
# Calculate interval between pairs
pair_interval = 1./rate - 10*ms
print('Starting simulations for %s' % rate)
# Initial values
Nrns.v = V_rest
Nrns.v_lowpass1 = V_rest
Nrns.v_lowpass2 = V_rest
Nrns.I_ext = 0*amp
Nrns.x_trace = 0.
Syn.w_ampa = init_weight
# loop over pairings
for ii in range(reps):
# 1st SPIKE
Nrns.v[0] = V_thresh + 1*mV
# 2nd SPIKE
run(10*ms)
Nrns.v[1] = V_thresh + 1*mV
# run
run(pair_interval)
print('Pair %d out of %d' % (ii+1, reps))
#store weight changes
weight_result[0, jj] = 100.*Syn.w_ampa[0]/init_weight
weight_result[1, jj] = 100.*Syn.w_ampa[1]/init_weight
################################################################################
# Plots
################################################################################
stitle = 'Pairings'
scolor = 'k'
figure(figsize=(8, 5))
plot(rate_array, weight_result[0,:], '-', linewidth=2, color=scolor)
plot(rate_array, weight_result[1,:], ':', linewidth=2, color=scolor)
xlabel('Pairing frequency [Hz]', fontsize=22)
ylabel('Normalised Weight [%]', fontsize=22)
legend(['Pre-Post', 'Post-Pre'], loc='best')
subplots_adjust(bottom=0.2, left=0.15, right=0.95, top=0.85)
title(stitle)
show()
