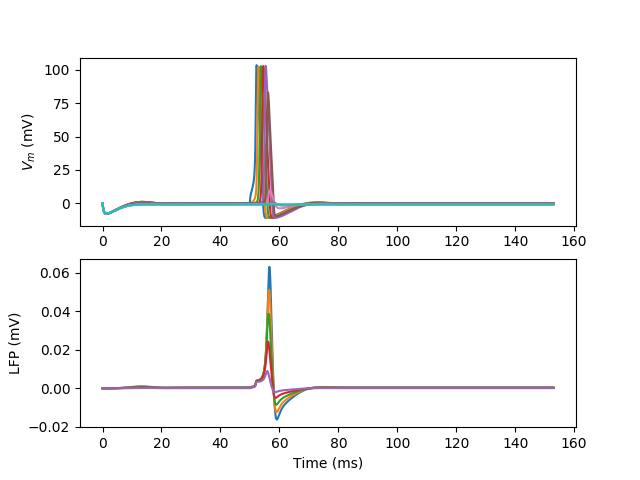
Example: lfp¶
Hodgkin-Huxley equations (1952)
We calculate the extracellular field potential at various places.
from brian2 import *
defaultclock.dt = 0.01*ms
morpho = Cylinder(x=[0, 10]*cm, diameter=2*238*um, n=1000, type='axon')
El = 10.613* mV
ENa = 115*mV
EK = -12*mV
gl = 0.3*msiemens/cm**2
gNa0 = 120*msiemens/cm**2
gK = 36*msiemens/cm**2
# Typical equations
eqs = '''
# The same equations for the whole neuron, but possibly different parameter values
# distributed transmembrane current
Im = gl * (El-v) + gNa * m**3 * h * (ENa-v) + gK * n**4 * (EK-v) : amp/meter**2
I : amp (point current) # applied current
dm/dt = alpham * (1-m) - betam * m : 1
dn/dt = alphan * (1-n) - betan * n : 1
dh/dt = alphah * (1-h) - betah * h : 1
alpham = (0.1/mV) * (-v+25*mV) / (exp((-v+25*mV) / (10*mV)) - 1)/ms : Hz
betam = 4 * exp(-v/(18*mV))/ms : Hz
alphah = 0.07 * exp(-v/(20*mV))/ms : Hz
betah = 1/(exp((-v+30*mV) / (10*mV)) + 1)/ms : Hz
alphan = (0.01/mV) * (-v+10*mV) / (exp((-v+10*mV) / (10*mV)) - 1)/ms : Hz
betan = 0.125*exp(-v/(80*mV))/ms : Hz
gNa : siemens/meter**2
'''
neuron = SpatialNeuron(morphology=morpho, model=eqs, Cm=1*uF/cm**2,
Ri=35.4*ohm*cm, method="exponential_euler")
neuron.v = 0*mV
neuron.h = 1
neuron.m = 0
neuron.n = .5
neuron.I = 0
neuron.gNa = gNa0
neuron[5*cm:10*cm].gNa = 0*siemens/cm**2
M = StateMonitor(neuron, 'v', record=True)
# LFP recorder
Ne = 5 # Number of electrodes
sigma = 0.3*siemens/meter # Resistivity of extracellular field (0.3-0.4 S/m)
lfp = NeuronGroup(Ne,model='''v : volt
x : meter
y : meter
z : meter''')
lfp.x = 7*cm # Off center (to be far from stimulating electrode)
lfp.y = [1*mm, 2*mm, 4*mm, 8*mm, 16*mm]
S = Synapses(neuron,lfp,model='''w : ohm*meter**2 (constant) # Weight in the LFP calculation
v_post = w*(Ic_pre-Im_pre) : volt (summed)''')
S.summed_updaters['v_post'].when = 'after_groups' # otherwise Ic has not yet been updated for the current time step.
S.connect()
S.w = 'area_pre/(4*pi*sigma)/((x_pre-x_post)**2+(y_pre-y_post)**2+(z_pre-z_post)**2)**.5'
Mlfp = StateMonitor(lfp,'v',record=True)
run(50*ms, report='text')
neuron.I[0] = 1*uA # current injection at one end
run(3*ms)
neuron.I = 0*amp
run(100*ms, report='text')
subplot(211)
for i in range(10):
plot(M.t/ms,M.v[i*100]/mV)
ylabel('$V_m$ (mV)')
subplot(212)
for i in range(5):
plot(M.t/ms,Mlfp.v[i]/mV)
ylabel('LFP (mV)')
xlabel('Time (ms)')
show()