Example: Clopath_et_al_2010_homeostasisΒΆ
Note
You can launch an interactive, editable version of this example without installing any local files using the Binder service (although note that at some times this may be slow or fail to open):
This code contains an adapted version of the voltage-dependent triplet STDP rule from: Clopath et al., Connectivity reflects coding: a model of voltage-based STDP with homeostasis, Nature Neuroscience, 2010 (http://dx.doi.org/10.1038/nn.2479)
The plasticity rule is adapted for a leaky integrate & fire model in Brian2.
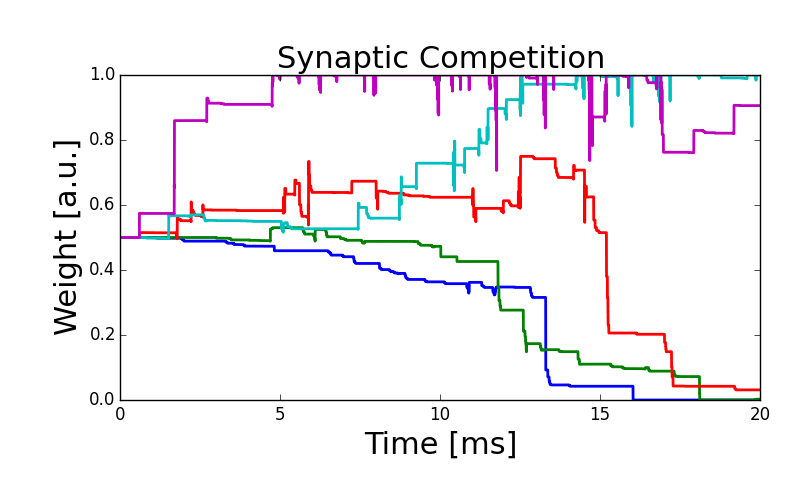
As an illustration of the rule, we simulate the competition between inputs projecting on a downstream neuron
We kindly ask to cite the article when using the model presented below.
This code was written by Jacopo Bono, 12/2015
from brian2 import *
################################################################################
# PLASTICITY MODEL
################################################################################
#### Plasticity Parameters
V_rest = -70.*mV # resting potential
V_thresh = -55.*mV # spiking threshold
Theta_low = V_rest # depolarization threshold for plasticity
x_reset = 1. # spike trace reset value
taux = 15.*ms # spike trace time constant
A_LTD = 1.5e-4 # depression amplitude
A_LTP = 1.5e-2 # potentiation amplitude
tau_lowpass1 = 40*ms # timeconstant for low-pass filtered voltage
tau_lowpass2 = 30*ms # timeconstant for low-pass filtered voltage
tau_homeo = 1000*ms # homeostatic timeconstant
v_target = 12*mV**2 # target depolarisation
#### Plasticity Equations
# equations executed at every timestep
Syn_model = ('''
w_ampa:1 # synaptic weight (ampa synapse)
''')
# equations executed only when a presynaptic spike occurs
Pre_eq = ('''
g_ampa_post += w_ampa*ampa_max_cond # increment synaptic conductance
A_LTD_u = A_LTD*(v_homeo**2/v_target) # metaplasticity
w_minus = A_LTD_u*(v_lowpass1_post/mV - Theta_low/mV)*(v_lowpass1_post/mV - Theta_low/mV > 0) # synaptic depression
w_ampa = clip(w_ampa-w_minus,0,w_max) # hard bounds
''' )
# equations executed only when a postsynaptic spike occurs
Post_eq = ('''
v_lowpass1 += 10*mV # mimics the depolarisation effect due to a spike
v_lowpass2 += 10*mV # mimics the depolarisation effect due to a spike
v_homeo += 0.1*mV # mimics the depolarisation effect due to a spike
w_plus = A_LTP*x_trace_pre*(v_lowpass2_post/mV - Theta_low/mV)*(v_lowpass2_post/mV - Theta_low/mV > 0) # synaptic potentiation
w_ampa = clip(w_ampa+w_plus,0,w_max) # hard bounds
''' )
################################################################################
# I&F Parameters and equations
################################################################################
#### Neuron parameters
gleak = 30.*nS # leak conductance
C = 300.*pF # membrane capacitance
tau_AMPA = 2.*ms # AMPA synaptic timeconstant
E_AMPA = 0.*mV # reversal potential AMPA
ampa_max_cond = 5.e-8*siemens # Ampa maximal conductance
w_max = 1. # maximal ampa weight
#### Neuron Equations
# We connect 10 presynaptic neurons to 1 downstream neuron
# downstream neuron
eqs_neurons = '''
dv/dt = (gleak*(V_rest-v) + I_ext + I_syn)/C: volt # voltage
dv_lowpass1/dt = (v-v_lowpass1)/tau_lowpass1 : volt # low-pass filter of the voltage
dv_lowpass2/dt = (v-v_lowpass2)/tau_lowpass2 : volt # low-pass filter of the voltage
dv_homeo/dt = (v-V_rest-v_homeo)/tau_homeo : volt # low-pass filter of the voltage
I_ext : amp # external current
I_syn = g_ampa*(E_AMPA-v): amp # synaptic current
dg_ampa/dt = -g_ampa/tau_AMPA : siemens # synaptic conductance
dx_trace/dt = -x_trace/taux :1 # spike trace
'''
# input neurons
eqs_inputs = '''
dv/dt = gleak*(V_rest-v)/C: volt # voltage
dx_trace/dt = -x_trace/taux :1 # spike trace
rates : Hz # input rates
selected_index : integer (shared) # active neuron
'''
################################################################################
# Simulation
################################################################################
#### Parameters
defaultclock.dt = 500.*us # timestep
Nr_neurons = 1 # Number of downstream neurons
Nr_inputs = 5 # Number of input neurons
input_rate = 35*Hz # Rates
init_weight = 0.5 # initial synaptic weight
final_t = 20.*second # end of simulation
input_time = 100.*ms # duration of an input
#### Create neuron objects
Nrn_downstream = NeuronGroup(Nr_neurons, eqs_neurons, threshold='v>V_thresh',
reset='v=V_rest;x_trace+=x_reset/(taux/ms)',
method='euler')
Nrns_input = NeuronGroup(Nr_inputs, eqs_inputs, threshold='rand()<rates*dt',
reset='v=V_rest;x_trace+=x_reset/(taux/ms)',
method='linear')
#### create Synapses
Syn = Synapses(Nrns_input, Nrn_downstream,
model=Syn_model,
on_pre=Pre_eq,
on_post=Post_eq
)
Syn.connect(i=numpy.arange(Nr_inputs), j=0)
#### Monitors and storage
W_evolution = StateMonitor(Syn, 'w_ampa', record=True)
#### Run
# Initial values
Nrn_downstream.v = V_rest
Nrn_downstream.v_lowpass1 = V_rest
Nrn_downstream.v_lowpass2 = V_rest
Nrn_downstream.v_homeo = 0
Nrn_downstream.I_ext = 0.*amp
Nrn_downstream.x_trace = 0.
Nrns_input.v = V_rest
Nrns_input.x_trace = 0.
Syn.w_ampa = init_weight
# Switch on a different input every 100ms
Nrns_input.run_regularly('''
selected_index = int(floor(rand()*Nr_inputs))
rates = input_rate * int(selected_index == i) # All rates are zero except for the selected neuron
''', dt=input_time)
run(final_t, report='text')
################################################################################
# Plots
################################################################################
stitle = 'Synaptic Competition'
fig = figure(figsize=(8, 5))
for kk in range(Nr_inputs):
plt.plot(W_evolution.t, W_evolution.w_ampa[kk], '-', linewidth=2)
xlabel('Time [ms]', fontsize=22)
ylabel('Weight [a.u.]', fontsize=22)
plt.subplots_adjust(bottom=0.2, left=0.15, right=0.95, top=0.85)
title(stitle, fontsize=22)
plt.show()
