Example: Diesmann_et_al_1999¶
Synfire chains¶
M. Diesmann et al. (1999). Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529-533.
from brian2 import *
duration = 100*ms
# Neuron model parameters
Vr = -70*mV
Vt = -55*mV
taum = 10*ms
taupsp = 0.325*ms
weight = 4.86*mV
# Neuron model
eqs = Equations('''
dV/dt = (-(V-Vr)+x)*(1./taum) : volt
dx/dt = (-x+y)*(1./taupsp) : volt
dy/dt = -y*(1./taupsp)+25.27*mV/ms+
(39.24*mV/ms**0.5)*xi : volt
''')
# Neuron groups
n_groups = 10
group_size = 100
P = NeuronGroup(N=n_groups*group_size, model=eqs,
threshold='V>Vt', reset='V=Vr', refractory=1*ms,
method='euler')
Pinput = SpikeGeneratorGroup(85, np.arange(85),
np.random.randn(85)*1*ms + 50*ms)
# The network structure
S = Synapses(P, P, on_pre='y+=weight')
S.connect(j='k for k in range((int(i/group_size)+1)*group_size, (int(i/group_size)+2)*group_size) '
'if i<N_pre-group_size')
Sinput = Synapses(Pinput, P[:group_size], on_pre='y+=weight')
Sinput.connect()
# Record the spikes
Mgp = SpikeMonitor(P)
Minput = SpikeMonitor(Pinput)
# Setup the network, and run it
P.V = 'Vr + rand() * (Vt - Vr)'
run(duration)
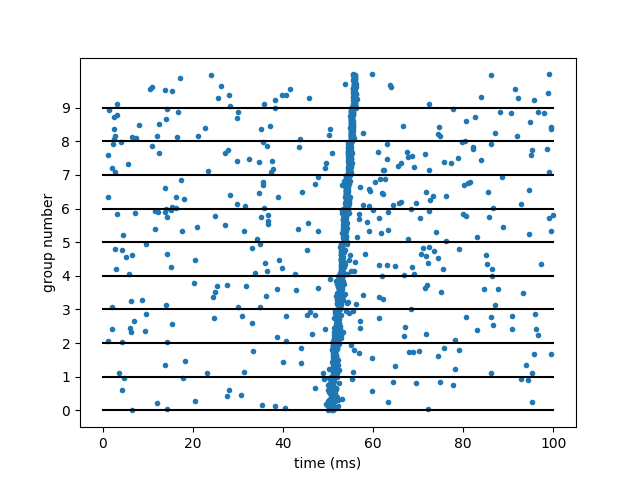
plot(Mgp.t/ms, 1.0*Mgp.i/group_size, '.')
plot([0, duration/ms], np.arange(n_groups).repeat(2).reshape(-1, 2).T, 'k-')
ylabel('group number')
yticks(np.arange(n_groups))
xlabel('time (ms)')
show()